Home Download Tutorial 1 Tutorial 2 Tutorial 3 Tutorial 4 Tutorial 5

One of the strength of ULySS is the set of tools included to help to study the parameters space. The problems handled with ULySS are non-linear and often complex enough to present degeneracies, multiple minima and restrictions on the convergence to the absolute minimum.
This page presents some examples of Monte-Carlo simulations, chi2 maps and convergence maps.

To follow this tutorial it is advisable first to read the general tutorial.

1. Monte-Carlo simulations

Monte-Carlo experiments are useful to visualize the degeneracies and validate the errors computed by the program from the covariance matrix by simulating the effect of the noise.
The Monte-Carlo simulations provided by ULYSS consists in repeating a loop where at each step a random Gaussian noise is added to the observation before the analysis. It produce an array of solution which can be exploited to measure the dispersion of the values of the parameters and view the degeneracies (correlations). The amplitude of the added noise is equal to the estimated noise attached to the observation (it is possibly different from pixel to pixel).
In this exercise we will first generate a composite stellar population spectrum made of two bursts (500 Myr and 10 Gyr). 
GDL> grid=uly_ssp_read(uly_root+'/models/PHR_Elodie31.fits', SIGMA=50., VELSCALE=50.)
GDL> young = uly_ssp_interp(grid, [alog(500.), 0.])
GDL> old = uly_ssp_interp(grid, [alog(10000.), -1.])
GDL> 
GDL> spectrum = uly_spect_alloc(DATA=0.1*young+0.9*old, START=grid.start, STEP=grid.step, SAMPLING=1)
We can check now that ULYSS can retrieve this information (easy case since no noise is added and the analysis is made with the model used to simulate the observation). 
GDL> cmp1 = uly_ssp(AG=[500.], ZG=[0], AL=[200.,3000.])
GDL> cmp2 = uly_ssp(AG=[10000.], ZG=[-1.], AL=[3000., 12000.])
GDL> cmp = [cmp1, cmp2]
GDL> ulyss, spectrum, cmp

Read the model ./models/PHR_Elodie31.fits
read the file ./models/PHR_Elodie31.fits
model reading time=       1.7927818
Convolve the model with Gaussian, sigma=      50.0000 km/s
model deriving time=      0.22342515
--------------------------------------------------------------------
INPUT PARAMETERS
--------------------------------------------------------------------
Name of the output file              output.res
Degree of multiplicative polynomial            10
No additive polynomial  
Component1 (cmp1) model:./models/PHR_Elodie31.fits 
  Guess for age: 500.00000 [Myr], Fe/H: 0.0000000 [dex]
Component2 (cmp2) model:./models/PHR_Elodie31.fits 
  Guess for age: 10000.000 [Myr], Fe/H: -1.0000000 [dex]
--------------------------------------------------------------------
Read the model ./models/PHR_Elodie31.fits
read the file ./models/PHR_Elodie31.fits
model reading time=       1.7861340
model deriving time=      0.22379780
Read the model ./models/PHR_Elodie31.fits
read the file ./models/PHR_Elodie31.fits
model reading time=       1.7899010
model deriving time=      0.22375083
--------------------------------------------------------------------
PARAMETERS PASSED TO ULY_FIT
--------------------------------------------------------------------
Wavelength range used                 :       3900.2252       6801.1087
 [Angstrom]
Sampling in log wavelength            :       50.000000 [km/s]
Number of independent pixels in signal:        3334
Number of pixels fitted               :        3334
DOF factor                            :      1.00000
--------------------------------------------------------------------
number of model evaluations:          12
time=      0.20227480
Number of pixels used for the fit        3269

cz             :       0.0000000 +/- 0.00062760970 km/s
dispersion     :       50.000000 +/- 0.00068582551 km/s
-----------------------------------------------
estimated SNR  :       54810.876
-----------------------------------------------
cmp #0  cmp1
Light fraction :       48.695512 +/-      0.014961593 %
Weight         :     0.099943584 +/-    3.0707454e-05 [data_unit/cmp_unit]
age            :       500.00000 +/- 0.022189165 Myr
Fe/H           :       0.0000000 +/- 3.9526592e-05 dex
-----------------------------------------------
cmp #1  cmp2
Light fraction :       51.304488 +/-      0.015264779 %
Weight         :      0.90047556 +/-    0.00026792121 [data_unit/cmp_unit]
age            :       10000.000 +/- 1.7618713 Myr
Fe/H           :      -1.0000000 +/- 4.6371446e-05 dex
-----------------------------------------------
And now we can run a Monte-Carlo simulation. We simply have to give the keyword NSIMUL to specify the number of simulations. Since we did not give an error spectrum in the simulation, a default S/N value (SNR=100) is assumed. 
GDL> ulyss, spectrum, cmp, NSIMUL=500, SNR=100, FILE_OUT='tuto_chi', /QUIET, /PLOT
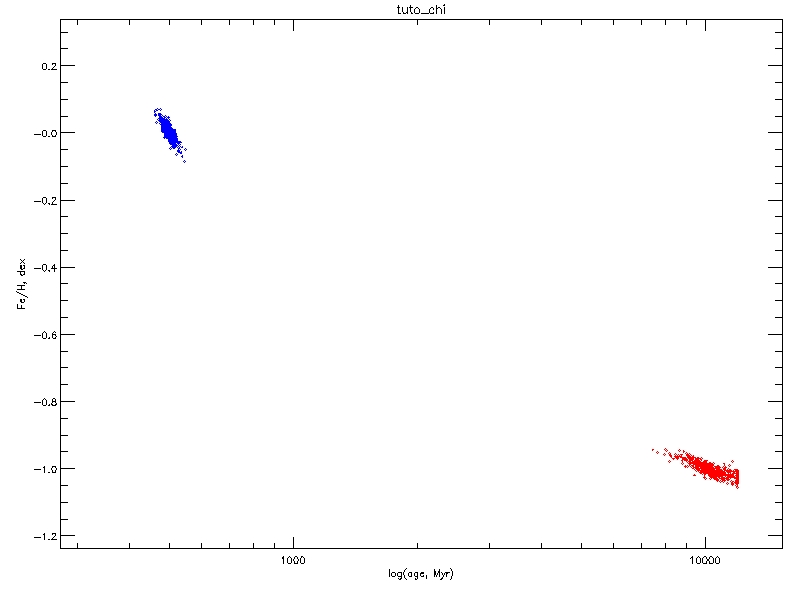
All the projections were plotted by default (in the present case 28 projections, because there are 8 free parameters: cz, sigma and for each of the 2 bursts, weight, age and metallicity).
We can plot a specfic projection (age-metallicity) where the two bursts overimposed with different colors: 
GDL> uly_solut_tplot, 'tuto_chi', XAXIS=4, YAXIS=5, XRANGE=[300.,14000.], YRANGE=[-1.2, 0.3], /XLOG
GDL> uly_solut_tplot, 'tuto_chi', XAXIS=7, YAXIS=8, /OVER, LINECOLOR='red'
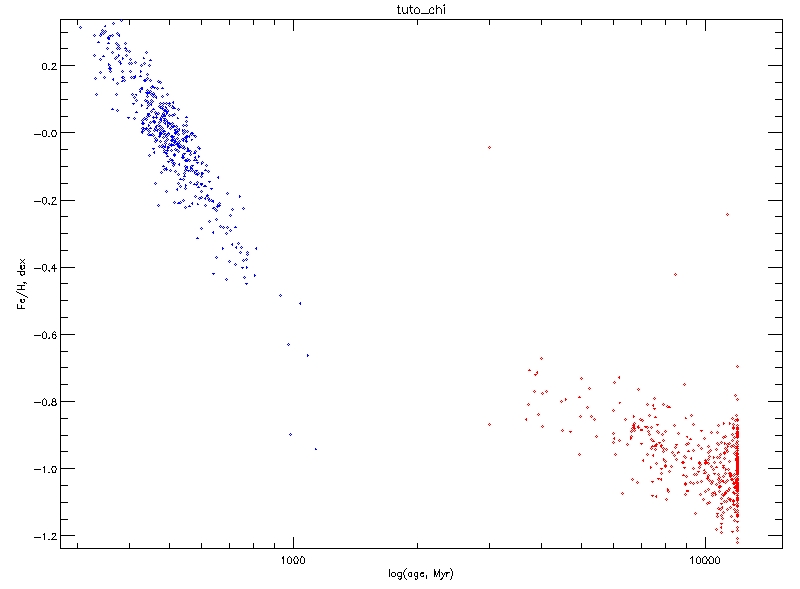
We can check the effect of a much larger noise (SNR=15); 
GDL> ulyss, spectrum, cmp, NSIMUL=500, FILE_OUT='tuto_chi', SNR=15, /QUIET
GDL> uly_solut_tplot, 'tuto_chi', XAXIS=4, YAXIS=5, XRANGE=[300.,14000.], YRANGE=[-1.2, 0.3], /XLOG
GDL> uly_solut_tplot, 'tuto_chi', XAXIS=7, YAXIS=8, /OVER, LINECOLOR='red'

2. Chi2 maps

Chi2 maps allow to visualize the location of eventual local minima and gives a view of the topology of the parameters space. A map is a 2D projection of the parameter's space, at each node of it, all the other parameters (if any) are optimized. Any local minimum can be identified on such map.
Lets continue here from the previous example and build the age-metallicity chi2 maps for the two bursts: 
GDL> chi1 = uly_chimap(spectrum, cmp, [[0,0],[0,1]])
GDL> chi2 = uly_chimap(spectrum, cmp, [[1,0],[1,1]])
GDL> window, 0
GDL> uly_chimap_plot, chi1, /XLOG, YRANGE=[-1.2, 0.3]
GDL> window, 1
GDL> uly_chimap_plot, chi2, /XLOG, YRANGE=[-1.2, 0.3]
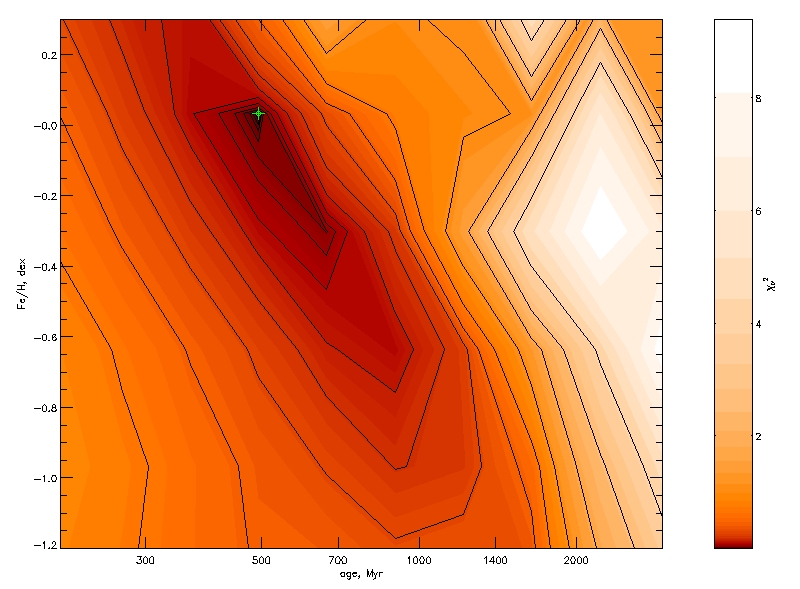
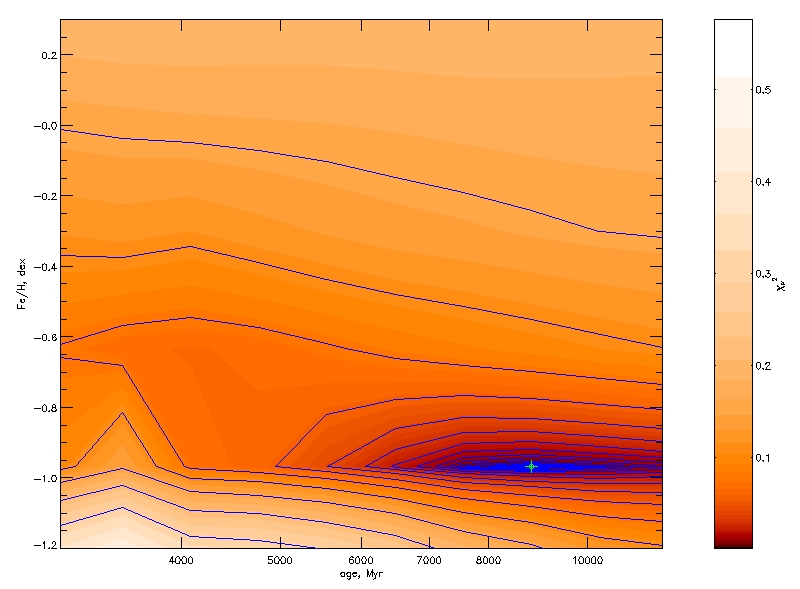
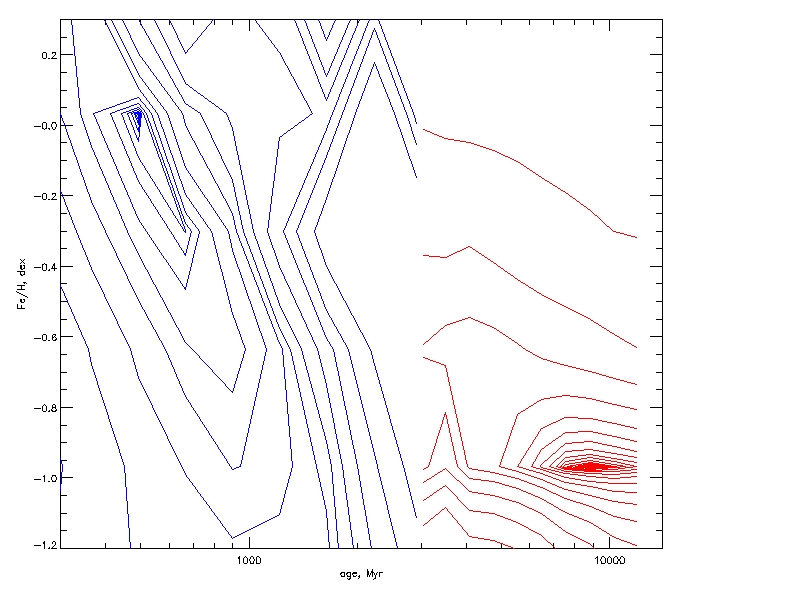
And plot only the contours on the same frame for the two bursts: 
GDL> uly_chimap_plot, chi1, XRANGE=[300.,14000.], /XLOG, YRANGE=[-1.2, 0.3], /HIDEHALFTONE, /HIDEMINIMA
GDL> uly_chimap_plot, chi2, /HIDEHALFTONE, /HIDEMINIMA, /OVER, LINECOLOR='red'

3. Convergence maps

Another tool to explore the parameters space is to investigate how the program converge to a solution from a grid of guesses. Ideally, we would like that the solution is stable whatever the guesses are. But, because of the local minima and degeneracies, it may not be the case. Below we perform a multiple local minimization from a grid of guesses, we store all the solutions in a file and we plot the convergence map: 
GDL> gal=uly_root+'/data/VazMiles_z-0.40t07.94.fits'
GDL> cmp = uly_ssp(AG=[500d,1000d,2000d,4000d,8000d,15000d,18000d], ZG=[-2d,-1.5d,-1d,-0.5d,0d,0.3d])
GDL> ulyss, gal, cmp, /ALL_SOL, FIL='absolute'
GDL> uly_solut_tplot, 'absolute.res', XA=[0,0], YA=[0,1], XR=[300,25000], YR=[-1.6,0.5], /CV, /XLOG
Contact: ulyss at obs.univ-lyon1.fr Last modified: Thu Jul 31 13:57:09 2008.